Stefano Giomo - The speLL game and spellops

The story behind the `speLL`

speLL stands for Single Pipeline L-chain, a streamlined approach to chaining fastcore’s L operations that ensure your data transformations are clean, readable, and maintainable (L is a powerful list-like container). The idea for the speLL emerged when I was practicing coding with AI to tackle Advent of Code (AoC) puzzles. Initially, I found myself writing code snippets like:

L(f_c(L(...).map(f_a).filter(f_b))).map(f_d)[0]

Although this worked, it was cumbersome to read, and the transformation order (f_a → filter(f_b) → f_c → f_d) was unclear, forcing you to break the pipeline for the sake of readability introducing intermediate variables.

t = L(...).map(f_a).filter(f_b)
L(f_c(t)).map(f_d)[0]

Wanting a cleaner syntax, I introduced the pipe operator so I could write:

L(...).map(f_a).filter(f_b).pipe(f_c).map(f_d)[0]

This was an improvement, but debugging remained frustrating. To see intermediate outputs, I’d comment out entire chunks of the chain:

L(...).map(f_a).filter(f_b)#.pipe(f_c).map(f_d)[0]    # This will inspect up to f_b

Then, I realized Python’s parentheses allow multiline chaining without extra syntactic fuss:

(L(...)    # input
    .map(f_a)    # apply f_a
    .filter(f_b) # filter by f_b
    .pipe(f_c)   # apply f_c
    .map(f_d)[0] # final step
)

From there, I introduced the tee to document and inspect any step in the chain, making these annotations persistent rather than transient, as comments often are:

(L(...)             .tee('input data')
    .map(f_a)       .tee('apply f_a to individual elements')
    .filter(f_b)    .tee('filter by f_b')
    .pipe(f_c)      .tee('apply f_c to the whole list')
    .map(f_d)[0]    .tee('finally apply f_d to the resulting elements and returning first value')
)

Finally, I added unwrap to safely and cleanly exit the pipeline. With these combined, I successfully solved multiple AoC puzzles in a “single line of code,” which I call a speLL.

*NOTE: Despite being spread across multiple lines using the (parentheses) trick, a speLL is still a one-statement. Of course, I’m not counting the definitions and tests of support functions ;-)

The speLL approach is designed not only for exploratory programming (i.e., enabling simple code modification, fluently laying out code from start to end of a pipeline, etc.) but also facilitates production-ready code that can be organized to be inspected live when needed (ie: with verbose=True):

def process(data, verbose=False):
    s = dict(show=verbose)
    
    # Customize state representation
    def display_as_table ...
    def print_and_write_to_disk ... 
    def display_as_image ...  

    return (L(...)
        .map(parse_line)       .tee('f_a: apply to individual elements', f=display_as_table, **s)
        .filter(is_valid)      .tee('f_b: filter valid ones', f=print_and_write_to_disk, **s)
        .pipe(summarize)       .tee('f_c: summarize the whole list', f=display_as_image, **s)
        .map(post_process)     .tee('f_d: post processing', **s)
        .unwrap()
    )

The speLL is not about code-golf ⛳️. Everything, including the L additions, emerged from tackling real problems (after all, we all want to help the AoC Elves save the day 😉) and from the need to reduce boilerplate while organizing code in a clear, linear, and understandable way.

The challenge and `spellops` library

I challenge you to try a different way of solving AoC puzzles - the speLL game. A speLL is a one-liner that harnesses the power of L operations (the LL is there as a reminder!) to summon the solution of a puzzle step in a clean, concise, and readable way, like a real Wizard ;-)

Let me share some examples and helpful tools to get you started:

# SPOILER ALERT: AoC 2024/1 part A
sample = '''3   4
4   3
2   5
1   3
3   9
3   3
'''

# The speLL
to_int_tuple = lambda a,b: (int(a),int(b)) # named lambda
def distance(a,b): return abs(a-b) # extract function

(L(sample.splitlines())
            .map(str.split)       # Split individual strings into two sub strings
            .starmap(to_int_tuple)    # Make an int out of string
            .zip(cycled=True)     # Same as zip*
            .map(sorted)          # Sorting individual lists
            .zip()                # Make a list of tuples from tuple of lists
            .starmap(distance)    # Compute distance for each tuple
            .sum()                # Summing distances
)

# RETURN: 11

Extract functions or name lambdas if they lead to important part of your solution, and test them independently: you’ll be surprised when it will works at first shot. I strongly recommend structuring the code this way, wrapping the (speLL) in parentheses. This will allow you to experiment with and debug intermediate steps more easily while keeping the code organized:

(L(sample.splitlines())
            .map(str.split)       # Split individual strings into two sub strings
            .starmap(to_int_tuple)    # Make an int out of string
            .zip(cycled=True)     # Same as zip*
            .map(sorted)          # Sorting individual lists
            #.zip()                # Make a list of tuples from tuple of lists
            #.starmap(distance)    # Compute distance for each tuple
            #.sum()                # Summing distances
)

# RETURN: (#2) [[1, 2, 3, 3, 3, 4],[3, 3, 3, 4, 5, 9]]

To make the speLL game possible and more enjoyable, I’ve created spellops, a small library that contains some fastcore.foundation.L additions:

Install from pip:

pip install spellops

This is the source code for the main contributions:

# spellops: a new set of fastcore L operators for creating speLL

from fastcore.foundation import L,patch

@patch
def pipe(self:L, f, wrap=True): return self._new(f(self)) if wrap else f(self)
@patch
def starpipe(self:L, f, wrap=True): return self._new(f(*self)) if wrap else f(*self)
@patch
def unwrap(self:L): 
    if len(self)==0: return None # nothing to return 
    if len(self)!=1: raise ValueError("Can't unwrap list with more than one element")
    return self[0]
def _default_print(x, msg=None, sep='\n', **kwargs): print(f"{msg+sep if msg else ''}{x}")
@patch
def tee(self:L, msg=None, f=_default_print, show=True, **kwargs): 
    if show: f(self, **kwargs) if msg is None else f(self, msg, **kwargs)
    return self

Main operators:

pipe(f): Transform the entire L using function f, staying in L-world (e.g., L([1,2,3]).pipe(sum) # L([6]))
starpipe(f): Like pipe but unpacks L as arguments (e.g., L([{1,2},{2,3}]).starpipe(set.intersection) # L([2]))
unwrap(): Get single result or None, error if multiple elements (e.g., L([42]).unwrap() # 42)
tee(msg): Debug/log current L state and continue chain (e.g., L([1,2]).tee("values") # prints and returns L([1,2]))

This is a speLL using the new tee operator to document code and results:

# SPOILER ALERT: AoC 2024/1 part A
(L(sample.splitlines())
            .map(str.split)       .tee('Split individual strings into two sub strings')
            .starmap(to_int_tuple)    .tee('Make an int out of string')
            .zip(cycled=True)     .tee('Same as zip*')
            .map(sorted)          .tee('Sorting individual lists')
            .zip()                .tee('Make a list of tuples from tuple of lists')
            .starmap(distance)    .tee('Compute distance for each tuple')
            .sum()                # Summing distances
)

Split individual strings into two sub strings
[['3', '4'], ['4', '3'], ['2', '5'], ['1', '3'], ['3', '9'], ['3', '3']]
Make an int out of string
[(3, 4), (4, 3), (2, 5), (1, 3), (3, 9), (3, 3)]
Same as zip*
[(3, 4, 2, 1, 3, 3), (4, 3, 5, 3, 9, 3)]
Sorting individual lists
[[1, 2, 3, 3, 3, 4], [3, 3, 3, 4, 5, 9]]
Make a list of tuples from tuple of lists
[(1, 3), (2, 3), (3, 3), (3, 4), (3, 5), (4, 9)]
Compute distance for each tuple
[2, 1, 0, 1, 2, 5]

RETURN: 11

Here we use the new starpipe operator to apply a custom function instead of breaking the pipeline with a temporary variable:

# SPOILER ALERT: AoC 2024/1 part B

# This function will be "mapped" to individual elements
def to_int_tuple(a,b): return (int(a),int(b))

# this function acts on the whole list
def count_instances(As,Bs): return [(o,len([t for t in Bs if t==o])) for  o in As]

from math import prod
(L(sample.splitlines())
                .map(str.split)         .tee('input data')
                .starmap(to_int_tuple)  .tee('int to tuples')
                .zip(cycled=True)       .tee('tuple of lists')
                .starpipe(count_instances)  .tee('apply count_instances to the "whole list"')
                .map(prod)              .tee('multiply tuple elements')
                .sum()
    )

input data
[['3', '4'], ['4', '3'], ['2', '5'], ['1', '3'], ['3', '9'], ['3', '3']]
int to tuples
[(3, 4), (4, 3), (2, 5), (1, 3), (3, 9), (3, 3)]
tuple of lists
[(3, 4, 2, 1, 3, 3), (4, 3, 5, 3, 9, 3)]
apply count_instances to the "whole list"
[(3, 3), (4, 1), (2, 0), (1, 0), (3, 3), (3, 3)]
multiply tuple elements
[9, 4, 0, 0, 9, 9]

RETURN: 31

This is another example showing the usage of pipe, starpipe, unwrap, tee:

s = dict(sep='\n= ', show=True)

# Count the number of common elements in two lists
(L([[1,2,3,2,7],[2,4,1]])
    .map(set)       .tee('transform lists in sets',**s)
    .starpipe(set.intersection)     .tee('intersect them using standard operator',**s)
    .pipe(len)      .tee('count number of common items',**s)
    .unwrap()       # stop the chain and return the value
)

transform lists in sets
= [{1, 2, 3, 7}, {1, 2, 4}]
intersect them using standard operator
= [1, 2]
count number of common items
= [2]

RETURN: 2

This example shows how to use advanced tee:

import numpy as np

def print_as_matrix(x:L, msg):
    print(msg)
    N = len(x)
    rows = len(x[0])
    for r in range(rows):
        row_str = (L([o[r] for o in x])
                        .map(lambda o: ''.join(map(str,o)))
                        .pipe(lambda x:'  '.join(x),wrap=False))
        print(row_str)

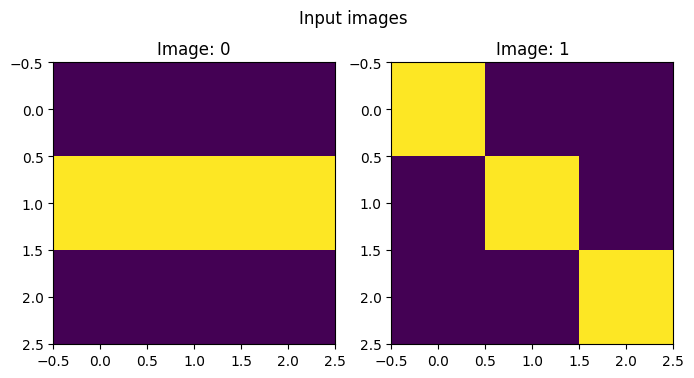
# Sums all the values of the first row of all matrices after rotating them of 90 degree
(L([[[0,0,0],[1,1,1],[0,0,0]],[[1,0,0],[0,1,0],[0,0,1]]])   .tee('Input images',f=print_as_matrix)
    .map(lambda x: np.rot90(x,k=1))     .tee('Rotate 90 degree',f=print_as_matrix)
    .map(lambda x: x[0].tolist())       .tee('Take first row')
    .map(sum)                           .tee('Sum element in list')
    .sum()
)

Input images
000  100
111  010
000  001
Rotate 90 degree
010  001
010  010
010  100
Take first row
[[0, 1, 0], [0, 0, 1]]
Sum element in list
[1, 1]

RETURN: 2

Or if you want you can use matplotlib:

def plot_images(x:L, msg):
    N = len(x)
    plt.figure(figsize=(4*N,4))
    for i,o in enumerate(x):
        plt.subplot(1,N,i+1)
        plt.imshow(o)
        plt.title(f'Image: {i}')
    plt.suptitle(msg)

The story behind the speLL

The challenge and spellops library

The story behind the `speLL`

The challenge and `spellops` library